Medidas de tendencia central (promedios)
                                                                         Media aritmética:

Mediana:

Moda:

Medidas de posición: 

Cuartiles:

Deciles:

Percentil:

Medidas de Dispersión:

Desviación Media:

Desviación Típica:

Varianza:

Medidas de Forma:

Asimetría y Curtosis:

Otra medida de forma:
"Curtosis"las medidas de curtosis tratan de estudiar la proporción de la varianza que se explica por la combinación de datos extremos respecto a la media en contraposición con datos poco alejados de la misma. Una mayor curtosis implica una mayor concentración de datos muy cerca de la media de la distribución coexistiendo al mismo tiempo con una relativamente elevada frecuencia de datos muy alejados de la misma. Esto explica una forma de la distribución de frecuencias con colas muy elevadas y con un centro muy apuntado.

Medidas de forma:
"Asimetría"es una propiedad de determinados cuerpos, funciones matemáticas y otros tipos de elementos en los que, al aplicarles una regla de transformación efectiva, se observan cambios respecto al elemento original. En estadística, el concepto de asimetría de una distribución indica la deformación horizontal de las distribuciones de frecuencia.Surge una discordia cuando no somos capaces de reconocer qué parte es la original de la asimetría.

Otra medida de dispersión:
"Desviación típica"La desviación típica es la raíz cuadrada de la varianza.

Es decir, la raíz cuadrada de la media de los cuadrados de las puntuaciones de desviación.

La desviación típica se representa por σ.

Desviación típica para datos agrupados

Para simplificar el cálculo vamos o utilizar las siguientes expresiones que son equivalentes a las anteriores.

"Varianza" La varianza es la media aritmética del cuadrado de las desviaciones respecto a la media de una distribución estadística.

La varianza se representa por .

Varianza para datos agrupados

Para simplificar el cálculo de la varianza vamos o utilizar las siguientes expresiones que son equivalentes a las anteriores.

Medidas de dispersión:

"Desviación Media" La desviación media es la media aritmética de los valores absolutos de las desviaciones respecto a la media.

La desviación media se representa por 

ejemplo:

Calcular la desviación media de la distribución:

9, 3, 8, 8, 9, 8, 9, 18

Desviación media para datos agrupados:

Si los datos vienen agrupados en una tabla de frecuencias, la expresión de la desviación media es:

Medidas de posición:
"Cuartiles":son los tres valores que dividen al conjunto de datos ordenados en cuatro partes porcentualmente iguales. 

Dada una serie de valores X₁,X₂,X₃ ...X_n ordenados en forma creciente, podemos pensar que su cálculo podría efectuarse:

Primer cuartil (Q₁) como la mediana de la primera mitad de valores;

Segundo cuartil (Q₂) como la propia mediana de la serie;

Tercer cuartil (Q₃) como la mediana de la segunda mitad de valores.

• Cálculo con datos no agrupados:
• Para el primer cuartil:



• Para el tercer cuartil:



"Deciles" son los nueve valores que dividen la serie de datos en diez partes iguales.

Los deciles se calculan como si fueran 10-cuartiles, o sea de manera que:
El primer decil separe el juego de datos entre el 10% de los valores inferiores, y el resto de los datos.
Y el noveno decil separe los datos entre el 90% de los valores inferiores y el 10% de los valores superiores.
"Percentiles" indica, una vez ordenados los datos de menor a mayor, el valor de la variable por debajo del cual se encuentra un porcentaje dado de observaciones en un grupo de observaciones. Por ejemplo, el percentil 20º es el valor debajo del cual se encuentran el 20 por ciento de las observaciones. Se representan con la letra P.

Parámetros Estadísticos: MEDIDAS DE TENDENCIA CENTRAL (PROMEDIOS)
"MEDIA ARITMÉTICA" es el valor característico de una serie de datos cuantitativos objeto de estudio que parte del principio de la esperanza matemática o valor esperado, se obtiene a partir de la suma de todos sus valores dividida entre el número de  sumandos. 
"MEDIANA" representa el valor de la variable de posición central en un conjunto de datos ordenados.

Datos sin agrupar:

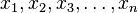Sean  los datos de una muestra ordenada en orden creciente y designando la mediana como 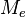, distinguimos dos casos:

a) Si n es impar, la mediana es el valor que ocupa la posición  una vez que los datos han sido ordenados (en orden creciente o decreciente), porque éste es el valor central. Es decir: .

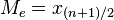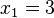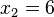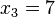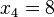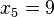Por ejemplo, si tenemos 5 datos, que ordenados son: , , , ,  => El valor central es el tercero: 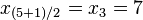. Este valor, que es la mediana de ese conjunto de datos, deja dos datos por debajo (, ) y otros dos por encima de él (, ).

Datos agrupados:

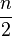Al tratar con datos agrupados, si  coincide con el valor de una frecuencia acumulada, el valor de la mediana coincidirá con la abscisa correspondiente. Si no coincide con el valor de ninguna abcisa, se calcula a través de semejanza de triángulos en el histograma o polígono de frecuencias acumuladas, utilizando la siguiente equivalencia: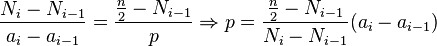

Donde  y 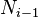 son las frecuencias absolutas acumuladas tales que ,  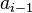y  son los extremos, interior y exterior, del intervalo donde se alcanza la mediana y 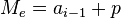 es la abscisa a calcular, la mediana. Se observa que  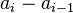es la amplitud de los intervalos seleccionados para el diagrama

"MODA" es el valor con una mayor frecuencia en una distribución de datos. EJE: 3-5-5-5-8-5-10-5-5 MO= 5